[無料ダウンロード！ √] 数学 円周角 問題 320458

円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

 この問題はそれを意識してみました。 特に北海道では「は？ 」という証明が出されることが他県に比べて多いので，満点取りたいなら慣れておきましょう。 円周角証明の究極系 目標時間：6分 難易度：★★★★☆ 範囲：中3円周角 ＜問題＞ ＜PDF，解答 こんにちは！レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 19年の大阪教育大学附属高等学校平野校舎の過去問より。 円周角の定理を使った良い問題だと思います。 持っている知識を生かして柔軟に考えてみて下さい！ ヒント 答え 詳しい解説 ① 状況把握 ②

数学 円周角 問題

数学 円周角 問題-円周角 補助線を引く問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 2つの半径oa, obと弦abによって できる三角形は必ず二等辺三角形になる。今年度の静岡県の入試で，丁度よい円周角の証明問題を発見したので，紹介します。 来年度からの北海道，これぐらいの難易度の証明だしそう。 「円周角の練習問題」 出典：令和3年度 静岡県 高校入試 数学 過去問 範囲：中3円周角 難易度：★★★★☆

6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4

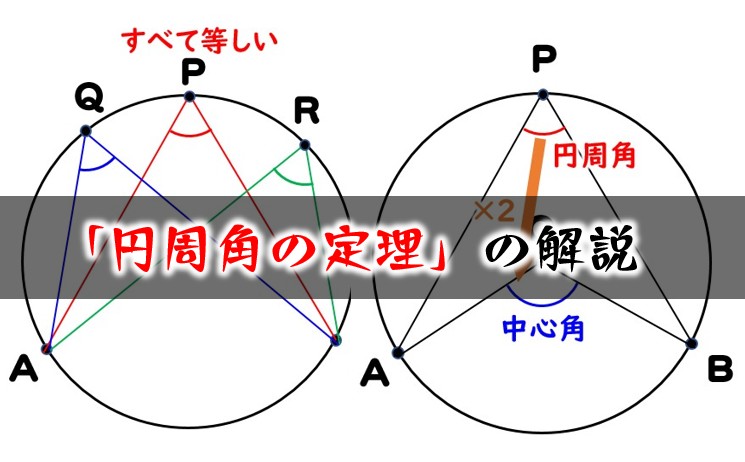
 円周角の定理に関する基本的な問題です。基本事項下の図のように 一つの孤に対する「円周角」の大きさは，「中心角」の半分になります． 同じ弧に対する円周角は等しくなります。覚えるのはこの2点だけです。 このような形になっている場合も円周角は中心角の半分になります。円周角の定理 はたったの 2 つだけです。 簡単なので、しっかり確認しましょう。 定理 1 ： 1 つの弧に対する円周角は中心角の半分 定理 2 ： 1 つの弧に対する円周角はすべて等しい ∠ A Q B = ∠ A P B = ∠ A R B (すべて AB ⌢ に対する円周角) 1：10 例題 10 弧の、円周に対する割合がわかれば中心角を求められる。 （かき込み） 教訓4： 円周に対する弧の 割合がわかる問題は、まず中心角を求める 例題7： 数学の問題を解くときの鉄則として、与えられらた条件をどこかで使わないと問題は解けません。

数学の学習の中でも証明が日常の役に立つことを実感し ている生徒は少ない。また中学校の数学の中で，円周角の定理を日常生活の中で用いる 場面を取り上げることはほぼないと感じる。そこで円周角の定理を用いた証明問題を取 り上げる。 中3数学 円周角（ブーメラン型四角形）まとめと問題 円周角の問題を解くとき、円周角の定理がわかっていても、どう解いたらいいのか悩むことも多いです。 今回はそんな円周角の中でも、ブーメラン型の四角形（凹四角形）の円周角について学習します 16年12月5日 / Last updated 16年12月5日 parako 数学 中3数学 円（円周角の定理） 円と相似 円と相似に関する問題です。 円周角の定理を利用して、相似な三角形の証明をしたり、相似比を利用して長さを求めたりします。

数学 円周角 問題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「数学 円周角 問題」の画像ギャラリー、詳細は各画像をクリックしてください。

円周角と中心角を使う円と半円の問題｜中学数学の定期テスト対策 中学数学の定期テスト対策の範囲です。 円周角と中心角を使う円と半円の問題｜高校入試レベルの難問まで 三平方の定理や面積比などもからめた、高校入試で見かける問題です。 円周角の定理は円の内側で考える問題でよく使われます。 同じ弧からピザが出ていた時は円周角の定理が使えます。 同じ弧を見つけることがポイントです。 補足メモ 同じ弧が別の場所にある問題を応用問題で作りたい。